Основа теории законы Кулона, открытые еще в 17 веке:
1. Если заряженный металлический шарик привести в
соприкосновение с поверхностью, какого либо, проводника, то заряд шарика
частично передается проводнику: шарик будет разряжаться до тех пор, пока их
потенциалы не выровняются.
2. Если шарик привести в соприкосновение с внутренней
поверхностью полого проводника. При этом весь заряд с шарика стечет на
проводник и распределится на внешней поверхности проводника.
В классике мы пользуемся устройствами, напряжение на которых
«ВЫРАВНИВАЕТСЯ». Рассмотрим первый вариант закона. Кстати весь закон сохранения
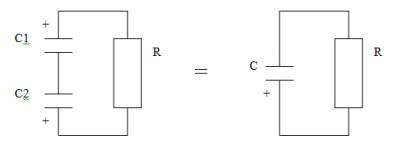
энергии построен именно на нем. Для примера возьмем два заряженных
конденсатора.
Рис. 1
Посчитаем энергии конденсаторов до слияния и энергии
конденсаторов после слияния:
Для наглядности я использую емкость конденсаторов в условных
единицах.
Допустим, что С1 = 5 ед. (Фарад), С2 = 15 ед. (Фарад).
Напряжение V1
= 15 вольт, а V2 = 30 вольт.
Энергия конденсаторов
считается по формуле : Е = (С * U * U) / 2
E1 =
(C1 * U1 * U1) / 2 = (5 * 15 * 15) / 2 = 562.5 ед. (джоулей).
E2 =
(C2 * U2 * U2) / 2 = (15 * 30 * 30) / 2 = 6750 ед. (джоулей).
Общая сумма энергий конденсаторов E(общая) = E1 + E2 = 562.5 + 6750 = 7312.5 ед. (джоулей).
Заряд конденсаторов считается по формуле : Q = C * U
Q1 =
C1 * U1 = 5 * 15 = 75 ед. (кулон).
Q2 =
C2 * U2 = 15 * 30 = 450 ед. (кулон).
После соединения конденсаторов, энергия на них
перераспределиться.
Для того, чтобы посчитать энергию, мы преобразуем два
конденсатора в один соединив их последовательно и добавим нагрузочный резистор,
для показа ухода энергии с конденсаторов.
Рис. 2
Посчитаем емкость последовательно соединенных конденсаторов:
С = (С1 * С2) / (С1 + С2) = (5 * 15) / (5 + 15) = 3.75 ед.
(Фарад).
Напряжение считаем по формуле : U = U1 + U2 =
15 + (-30) = -15 вольт.
Энергия общего конденсатора : E(C) = E(R) = (C * U * U) /
2 = (3.75 * (-15) * (-15)) / 2 = 421.875 ед. (джоулей).
Заряд общего конденсатора : Q = C * U =
3.75 * (-15) = -56.25 ед. (кулон).
Знак минус означает, что ток в схеме потечет в обратном
направлении относительно выбранной нами точки отсчета. При разряде общего
конденсатора, энергия E полностью высвободиться на резисторе R. Конденсатор С1 приобретет заряд Q, а конденсатор C2 потеряет точно такой же
заряд Q.
Посчитаем заряды конденсаторов С1 и С2 после
перераспределения зарядов.
Q1`
= Q1 + Q = 75 + 56.25 = 131.25 ед.
(кулон).
Q2`
= Q2 - Q = 450 – 56.25 = 393.75 ед.
(кулон).
Посчитаем напряжения на конденсаторах С1 и С2 после
перераспределения зарядов.
U1`
= Q1` / C1 = 131.25 / 5 = 26.25 вольт.
U2`
= Q2` / C2 = 393.75 / 15 = 26.25 вольт.
Равное напряжение на конденсаторах C1 и C2 соответствует 1-му закону, что означает верные вычисления.
Рассмотрим энергии конденсаторов после перераспределения
зарядов:
E1`
= (C1 * V1` * U1`) / 2 = (5 * 26.25 * 26.25) / 2 = 1722.65625 ед. (джоулей).
E2`
= (C2 * V1` * U2`) / 2 = (15 * 26.25 * 26.25) / 2 = 5167.96875 ед. (джоулей).
Проверим, равны ли энергии конденсаторов до распределения
зарядов и после распределения зарядов. Для этого просуммируем энергии
конденсаторов C1, C2 и энергии выделавшейся на
резисторе R:
E` =
E = E1` + E2 ` + E(R) = 1722.65625 + 5167.96875
+ 421.875 = 7312.5 ед. (джоулей).
Как видим энергии до распределения заряда и после
распределения заряда равны.
Значит, закон сохранения энергии работает, и с этим ничего
не поделаешь.
Первый закон, закон ВЫРАВНИВАНИЯ зарядов, всегда преследует
нас в любой классической схеме и всегда препятствует получению устройств с КПД >
1. В первом законе всегда преобразованная энергия будет равна начальной энергии,
за минус потерь преобразования таковой.
E`(начальная)
= E(преобразованная) + E(потерянная на
преобразовании).
Поэтому в любом устройстве, созданным по первому
закону, КПД будет всегда стремиться к 1
и никогда не достигнет ее. Это определяет постулат Великой физики, которую
признает современная наука.
Но есть и второй закон, который также известен, но никто его
не использует, потому, что это идет в разрез с законом сохранения энергии.
Устройства, построенные на втором законе, законе ПЕРЕТЕКАНИЯ заряда, всегда
работают на неравенствах.
Работу некого устройства, построенного на принципе второго
закона, давайте сейчас и разберем.
Для начала рассмотри, что за эффект все таки мы ищем в
устройствах Смита, Капанадзе, Стивена, но никак не можем найти. Во первых, мы
строим схему по первому закону и пытаемся что то понять в том, в чем в принципе
понять ничего нельзя. Нельзя покушаться на постулат первого закона, ничего не
выйдет, да и в принципе и не нужно, есть другой путь и другие постулаты,
которые нам еще нужно сформировать, т.к. устройства на втором законе вообще еще
никем не рассматривались. Эти устройства предают «анафеме», а их изобретателей
«сжигают на костре» или преследуют всю жизнь.
И так, начнем. Что нам дает второй закон.
Второй закон позволяет нам передать всю энергию менее
заряженного тела к энергии более заряженному телу. Что обеспечивает прирост
энергии более заряженного тела за счет менее заряженного, а соответственно
золотую формулу для устройств с КПД > 1.
E`(преобразованная)
= E(начальная первого)
+ E(начальная второго).
Поправка на формулу, энергия складывается путем сложения
зарядов первого и второго тела, за счет внутренних отталкивающих сил
возникающих в заряде.
Как видим в формуле нет потерь, а есть только эффект сложения
энергий. Этот эффект мы и будем использовать дальше.
Как видим в определении второго закона, нам нужно лишь заряд
положить внутрь полого проводника, и он сам до последнего электрона выйдет на
поверхность этого проводника. Единственное условие, которое нужно соблюсти во
втором законе, чтобы он заработал – это одноименность заряда, тогда он выйдет
на поверхность и энергии зарядов сложатся. Если мы будем работать с зарядами
разной полярности, получаемыми в результате их разделения, второй закон просто
не будет работать, заряды с поверхности втянутся внутрь проводника и
компенсируют друг друга.
Рассмотрим процесс, при котором можно «налить» электронов в
конденсатор, не тратя дополнительной энергии на преодоление электростатических
сил, точно так же как мы наполняем бочку водой. Для этого строим некое
устройство, которое позволит нам провести эксперимент доказывающий
работоспособность второго закона.
Берем два металлических цилиндра радиусом R1 = 5 и R2 = 15. Внешние поверхности, которых
соединяем проводящим материалом. Заряд обоих цилиндров равен 0. Для зарядки
этих цилиндров, берем металлический шарик радиусом 1 и потенциалом на его
поверхности Vш = 4
вольта. Заряжать цилиндры мы будем шариком, через внутреннюю поверхность
цилиндра R1. И так
вычислим емкости цилиндров и шарика.
Емкость шара рассчитывается по формуле : C = 4 * π * ε * ε0
* R, для простоты и наглядности расчета, я π, ε, ε0 возьму за единицу, т.к. это
константы, на искаженность расчетов эта замена не повлияет, можете сами
пересчитать правильно, тут главное сам принцип, а не расчет. Считать с
правильными константами будем, когда будем проектировать реальное устройство.
Еще раз повторяю, на сам принцип получения СЕ замена констант не влияет. И так
продолжим. Считаем емкость металлического шарика.
Сш = 4 * 1 = 4 ед. (Фарад).
Энергия шарика составляет: Eш = (Cш * Uш * Uш) / 2 = (4 * 4 * 4) /
2 = 32 ед. (джоулей).
Заряд шарика Qш
= Сш * Uш = 4 * 4 = 16
ед. (кулон).
Из расчетов видно, для того чтобы зарядить шарик до 4 вольт,
нужно потратить 32 ед. (джоулей) и 16 ед. (кулон). Соответственно, если шарик
разряжать через внутреннюю поверхность цилиндра R1, то для зарядки шарика до 4 вольт
потребуется одинаковое количество энергии. И каждый раз, когда мы будем
заряжать шарик из источника, нам потребуется взять 32 ед. * N(раз) ед. (джоулей) и 16 ед. * N(раз) ед. (кулонов). Тем
самым мы выяснили, что на каждом цикле заряда и разряда шарика у нас будет
линейная зависимость расхода энергии от источника. Теперь определим емкость
цилиндров R1 и R2. Емкость полого цилиндра
считается по тоже формуле, но признаюсь честно я ее не нашел ее в интернете при
написании данной статьи, а высчитывать ее специально просто лень, опять же по
какой формуле считается та или иная емкость здесь не важна, главное показать
Вам, дорогие мои читатели, сам принцип, а не формулы. Продолжим. Предположим,
что емкость Cr1 = 25 ед. (фарад), а Cr2 = 60 ед. (фарад). Общая емкость
данных цилиндров будет Собщ = Сr1
+ Cr2 = 25 + 60 = 85
ед. (фарад). Емкости суммируются потому, что заряды располагаются равномерно по
поверхности, как первого, так и второго цилиндров. И соответственно заряды будут
накапливаться на поверхности цилиндров, а распределятся между цилиндрами уже по
первому закону.
Рассмотрим процесс накопления зарядов на поверхности
цилиндров. Заряжаем шарик от внешнего источника (для исключения некоторых
вопросов, шарик всегда заряжаем от внешнего источника). Заряженный шарик
помещаем внутрь первого цилиндра и соединяем его к внутренней поверхности
такового. По второму закону, шарик полностью передает заряд в количестве 16
кулон на первый цилиндр. Первый цилиндр приобретает потенциал на поверхности в
соответствии с формулой Ur1
= Qr1 / Cr1 = 16 / 25 = 0.64 вольта.
Заряд с поверхности первого цилиндра постепенно перетекает на поверхность
второго до тех пор, пока их потенциалы на обоих цилиндрах не выровняется
(действует первый закон). Посчитаем потенциал после распределения зарядов Ur = Qr / Cr = 16 / 85 = 0.1882 (примерно равно) вольта. Энергия на
цилиндрах получается Er
= (Cr * Ur * Ur) / 2 = (85 * 0.1882 * 0.1882) / 2 =
1.5058 ед. (джоулей) (примерно с округлением). Если смотреть на затраченную
энергию которую сообщил шарику источник энергии, то получается КПД = Er / Eш = 1.5058 / 32 = 0.047 или 4.7%.
Что это такое скажите Вы, дорогие мои читатели, где сверх
единица, если КПД = 4,7%, но не будем спешить. Зарядим еще раз шарик и точно
также его разрядим через внутреннюю поверхность первого цилиндра. Цилиндры
обретут заряд уже в 32 ед. (кулон) (16 ед. кулон уже были на поверхности от
первого заряда и 16 пришли с вновь заряженного шарика), потенциал на их
поверхности повыситься уже до Ur
= 32 / 85 = 0.3764 вольт (примерно), энергия на цилиндрах будет равна Er = (85 * 0.3764 * 0.3764) /
2 = 6.02352, а КПД установки составит уже КПД = 6.02352 / 64 = 0.094 или 9.4%.
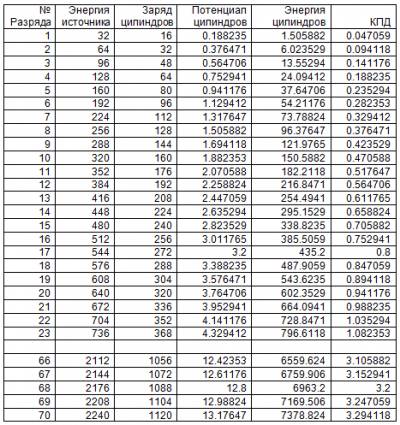
И так попробуем повторять заряды и разряды шарика на внутреннюю поверхность
первого цилиндра. Смотрим таблицу:
И так мы достигли затраченной
энергии от источника на 22 разрядке шарика на внутреннюю поверхность первого
цилиндра. На 43 разрядке энергия на цилиндрах уже превысила затраченную энергию
от источника в 2 раза, на 64 разрядке уже в 3 раза.
Шарик мы могли разрежать и на
внутреннюю поверхность второго цилиндра, разницы никакой нет, главное чтобы был
одинаковый потенциал. На шарике и цилиндрах.
Теперь немножко о главном.
Второй закон работает на законе
сохранения зарядов, закон сохранения энергии тут не работает. Вся фишка в том,
что энергия переноситься через заряды, которые можно переносить на разные
поверхности, меняя тем самым энергетику самих зарядов.
Конструктив с применением второго
закона может быть разный, боль на выдумку хитра. Главное суметь правильно
разделить заряды и исключить в схеме их взаимное влияние. Невыполнение этого
условия превратит цилиндры в обычный проводник, в кусок проводящего, никому не
нужного, материала.
Теперь о самом главном. Таким же
способом можно заряжать и обычные конденсаторы, только, что бы максимально
исключить влияние зарядов друг на друга, нужна уединенная емкость, т.е. земля.
Теперь понятно надеюсь, зачем Капанадзе нужна земля. Конструктив можно сделать и
без нее, просто нужно правильно поставить задачу.
Кстати забыл сказать, что в
качестве накачивающей емкости можно использовать и катушку, просто правильно ее
сконфигурируйте и замаскируйте и никто не догадается, что это обычный
конденсатор, даже если разберут устройство по молекулам.
Для обеспечения наглядности и
самого смысла приведу простой пример:
Пусть есть конденсатор С1
емкостью 100 единиц, заряженный 100 вольт
Заряд конденсатора Q1 = C1 * U1 =
100 * 100 = 10 000 ед кулонов
Энергия E1 = (C1 * U1 * U1) / 2 =
(100 * 100 * 100) / 2 = 500 000 ед. джоулей
но энергия равна 500 000 ед.
джоулей
Теперь берем кондер 10 единиц,
заряженный до 10 вольт
Q2 = C2 * U2 = 10 * 10 = 100 ед.
кулон
E2 = (C2 * U2 * U2) / 2 = (10 * 10 * 10) / 2 = 500 ед. джоулей
Да забыл сказать, что эти кондеры
допустим у нас шары, или цилиндры, в принципе не так важно. Теперь маленький
кондер помещаем внутрь большого и разряжаем его через внутреннюю поверхность
первого
со второго на первый перетекает
только заряд
Q1` = Q1 + Q2 = 10 000 + 100 = 10
100 ед. кулон
V1` = Q1` / C1 = 10 100 / 100 =
101 вольт
E1` = (C1 * U1` * U1`) / 2 = (100
* 101 * 101) / 2 = 510 050 ед. ждоулей
Теперь дельта энергий
дельта = 510 050 - 500 000 = 10
050 ед. джоулей
а энергию которую мы подвели
через С2 = 500 ед. джоулей
КПД посчитать?
В принципе все, что у меня есть.
С уважением Sorduck.
 Гостевая
Гостевая Админ
Админ Форум
Форум
 Юзеры
Юзеры